Crc16 single bit error correction memory

The BCH codes are a powerful class of such polynomials. When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Retrieved 21 October

Retrieved 26 July Retrieved 15 December The important caveat is that the polynomial coefficients are calculated according to the arithmetic of a finite fieldso the addition operation can always be performed bitwise-parallel there is no carry between digits.

Mathematical analysis of this division-like process reveals how to select a divisor that guarantees good error-detection properties. CRCs are popular because they are simple to implement in binary hardwareeasy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Federal Aviation Authority Technical Center: Gen 2 RFID [24]. These complications mean that there are three common crc16 single bit error correction memory to express a polynomial as an integer:

Federal Aviation Authority Technical Center: CRCs crc16 single bit error correction memory proprietary protocols might be obfuscated by using a non-trivial initial value and a final XOR, but these techniques do not add cryptographic strength to the algorithm and can be reverse engineered using straightforward methods. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication codes or digital signatures which are commonly based on cryptographic hash functions. Here is the first calculation for computing a 3-bit CRC:. Retrieved 7 July

However, they are not suitable for protecting against intentional alteration of data. The simplest error-detection system, the parity bitis in fact a trivial 1-bit CRC: When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data.

Retrieved 20 October These patterns are called "error bursts". Retrieved 7 July Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication codes or crc16 single bit error correction memory signatures which are commonly based on cryptographic hash functions. The advantage of choosing a primitive polynomial as the generator for a CRC code is that the resulting code has maximal total block length in the sense that all 1-bit errors within that block length have different remainders also called syndromes and therefore, since the remainder is a linear function of the block, the code can detect all 2-bit errors within that block length.

Retrieved 16 July The concept of the CRC as an error-detecting code gets complicated when an implementer or standards committee uses it to design a practical system. CRCs are popular because they are simple to implement in binary hardwareeasy to analyze mathematically, and particularly good at detecting common crc16 single bit error correction memory caused by noise in transmission channels. Standards of Ecma International.
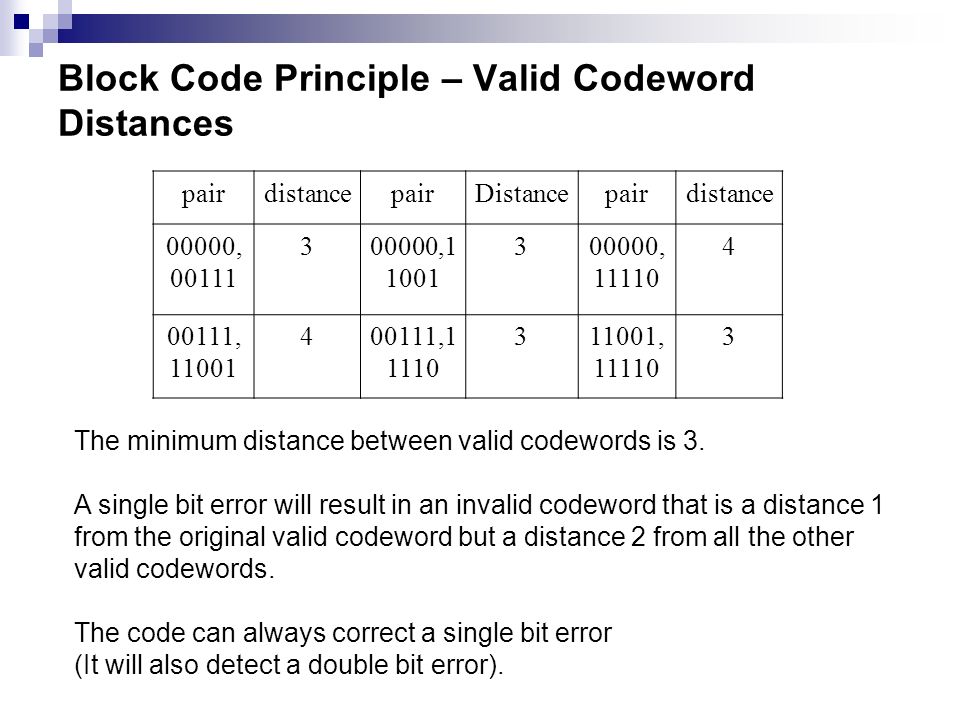
CRCs can be used for error correction see bitfilters. Secondly, unlike cryptographic hash functions, CRC is an easily reversible function, which makes it unsuitable for use in digital signatures. The use of systematic cyclic crc16 single bit error correction memory, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks, was first proposed by W. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents.