5 bit ripple counter with d
A counter circuit is usually constructed of a number of flip-flops connected in cascade. Counters are a very widely used component in digital circuitsand are manufactured as separate integrated circuits and also incorporated as parts of larger integrated circuits. In electronicscounters can be implemented quite easily using register-type circuits such as the flip-flopand a wide variety of classified into:.
Each is useful for different applications. Usually, counter circuits are digital in nature, and count in natural binary. Many types of counter circuits are available as digital building blocks, for example a number of chips in the series implement different counters. Occasionally there are advantages to using 5 bit ripple counter with d counting sequence other than the natural binary sequence—such as the binary coded decimal counter, a linear-feedback shift register counter, or a Gray-code counter.
Counters are useful for digital clocks and timers, and in oven timers, VCR clocks, etc. An asynchronous ripple counter is a single d-type flip-flopwith its J data input fed from its own inverted output. This circuit can store one bit, and hence can count from zero to one before it overflows starts over from 0. This counter will increment once for every clock cycle and takes two clock cycles to overflow, so every cycle it will alternate between a transition from 0 to 1 and a transition from 1 to 0.
5 bit ripple counter with d this output is then used as the clock signal for a similarly arranged D flip-flop remembering to invert the output to the inputone will get another 1 bit counter that counts half as fast.
Putting them together yields a two-bit counter:. You can continue to add additional flip-flops, always inverting the output to its own input, and using the output from the previous flip-flop as the clock signal. The result is called a ripple counter, which can count to 2 n - 1 where n is the number of bits flip-flop stages in the counter. Ripple counters suffer from unstable outputs as the overflows "ripple" from stage to stage, but they do find frequent application as dividers for clock signals, where the instantaneous count is unimportant, but the division ratio overall is to clarify this, a 1-bit counter is exactly equivalent to a divide by two circuit; the output frequency is exactly half that of the input when fed with a regular train of clock pulses.
The use of 5 bit ripple counter with d outputs as clocks leads to timing skew between the count data bits, making this ripple technique incompatible with normal synchronous circuit design styles. In synchronous counters, the clock inputs of all the flip-flops are connected together and are triggered by the input pulses. Thus, all the flip-flops change state simultaneously in parallel. The circuit below is a 4-bit synchronous counter. A simple way of implementing the logic for each bit of an ascending counter which is what is depicted in the adjacent image is for each bit to toggle when all of the less significant bits are at a 5 bit ripple counter with d high state.
For example, bit 1 toggles when bit 0 is logic high; bit 2 toggles when both bit 5 bit ripple counter with d and bit 0 are logic high; bit 3 toggles when bit 2, bit 1 and bit 0 are all high; and so on. Synchronous counters can also be implemented with hardware finite-state machineswhich are more complex but allow for smoother, more stable transitions.
A decade counter is one that counts in decimal digits, rather than binary. A decade counter may have each that is, it may count in binary-coded decimalas the integrated circuit did or other binary encodings. An ordinary four-stage counter can be easily modified to a decade counter by adding a NAND gate as in the schematic to the right. It counts from 0 to 9 and then resets to zero. The counter output can be set to zero by pulsing the reset line low.
The count then increments on each clock pulse until it reaches decimal 9. When it increments to decimal 10 both inputs of the NAND gate go high. The result is that the NAND output goes low, and resets the counter to zero. A ring counter is a circular shift register which is initiated such that only one of its flip-flops is the state one while others are in their zero states.
A ring counter is a shift register a 5 bit ripple counter with d connection of flip-flops with the output of the last one connected to the input of the first, that is, in a ring. Typically, a pattern consisting of a single bit is circulated so the state repeats every n clock cycles if n flip-flops are used.
These counters find specialist applications, including those similar to the decade counter, digital-to-analog conversion, etc. They can be implemented easily using D- or JK-type flip-flops. In computability theorya counter is considered a type of memory. A counter stores a single natural number initially zero and can be arbitrarily long. A 5 bit ripple counter with d is usually considered in conjunction with a finite-state machine FSMwhich can perform the following operations on the counter:.
The following machines are listed in order of power, with each one being strictly more powerful than the one below it:. For the first and last, it doesn't matter whether the FSM is a deterministic finite automaton or a nondeterministic finite automaton. They have the same power. The first two and the last one are levels of the Chomsky 5 bit ripple counter with d.
The first machine, an FSM plus two counters, is equivalent in power to a Turing machine. See the article on counter machines for a proof.
A web counter or hit counter is a computer software program that indicates the number of visitors, or hits, a particular webpage has received. Once set up, these counters will be incremented by one every time the web page is accessed in a web browser. The number is usually displayed as an inline digital image or in plain text or on a physical counter such as a mechanical counter. Images may be presented in a variety of fontsor 5 bit ripple counter with d the classic example is the wheels of an odometer.
Web counter was popular in the mid to late s and early s, 5 bit ripple counter with d replaced by more detailed and complete web traffic measures. Many automation systems use PC and laptops to monitor different parameters of machines and production data. Counters may count parameters such as the number of pieces produced, the production batch number, and measurements of the amounts of material used.
Long before electronics became common, mechanical devices were used to count events. These are known as tally counters. They typically consist of a series of disks mounted on an axle, with the digits 0 through 9 marked on their edge. The right most disk moves one increment with each event.
Each disk except the left-most has a protrusion that, after the completion of one revolution, moves the next disk to the left one increment. Such counters were used as odometers for bicycles and cars and in tape recordersfuel dispensersin production machinery as well as in other machinery.
One of the largest manufacturers was the Veeder-Root company, and their name was often used for this type of counter. Hand held tally counters are used mainly for stocktaking and for counting people attending events. Electromechanical counters were used to accumulate totals in tabulating machines that pioneered the data processing industry.
From Wikipedia, the free encyclopedia. This article is about the term counter used in electronics, computing, and mechanical counting devices. For other uses, see Counter disambiguation. The Art of Electronics. Modern Dictionary of Electronics. Retrieved from " https: Numeral systems Digital circuits Unary operations.
Views Read Edit View history. In other projects Wikimedia Commons. This page was 5 bit ripple counter with d edited on 3 Mayat By using this site, you agree to the Terms of Use and Privacy Policy.
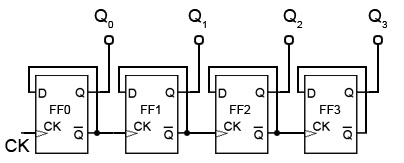
The Web This site. The output is a binary value whose value is equal to the number of pulses received at the CK input. Each output represents one bit of the output word, which, in 74 series counter ICs is usually 4 bits long, and the size of the output word depends on the number of flip-flops that make up the counter.
The output lines of a 4-bit counter represent the values 2 02 12 2 and 2 3or 1,2,4 and 8 respectively. They are normally shown in schematic diagrams in reverse order, with the least significant bit at the left, this is to enable the schematic diagram to show the circuit following the convention that signals flow from left to right, therefore in this case the CK input is at the left.
The rising edge of the Q output of each flip-flop triggers the CK input of the next flip-flop at half the frequency of the 5 bit ripple counter with d pulses applied to its input. The Q outputs then represent a four-bit binary count with Q 0 to Q 3 representing 2 0 1 to 2 3 8 respectively.
Assuming that the four Q outputs are initially atthe rising edge of the first CK pulse applied will cause the output Q 0 to go to logic 1, and the next CK pulse will make Q 0 output return to logic 0, and at the same time Q 0 will go from 0 to 1.
The next third CK pulse will cause Q 0 to go to logic 1 again, so both Q 0 and Q 1 will now be high, making the 4-bit output 2 3 10 remembering that Q 0 is the least significant bit. The fourth CK pulse will make both Q 0 and Q 1 return to 0 and as Q 1 will go high at this time, this 5 bit ripple counter with d toggle FF2, making Q 2 high and indicating 2 4 10 at the outputs. Reading the output word from right to left, the Q outputs therefore continue to represent a binary number equalling the number of input pulses received at the CK input of FF0.
As this is a four-stage counter the flip-flops will continue to toggle in sequence and the four Q outputs will output a sequence of binary values from 2 to 2 0 to 15 10 before the output returns to 2 and begins to count up again as illustrated by the waveforms in Fig 5.
To convert the up counter in Fig. By taking both the output lines and the CK pulse for the next flip-flop in sequence from the Q output as shown in Fig. Although both up and down counters can be built, using the asynchronous method for propagating the clock, they are not widely used as counters as they become unreliable at high clock speeds, or when a large number of flip-flops are connected together to give larger counts, due to the clock ripple effect. The effect of clock ripple in asynchronous counters is illustrated in Fig.
As the Q 0 to Q 3 outputs each change at different times, a number of different output states occur as any particular clock pulse causes a 5 bit ripple counter with d value to appear at the outputs. At CK pulse 8 for example, the outputs Q 0 to Q 3 should change from 2 7 10 to 2 8 10however what really happens reading the vertical columns of 1s and 0s in Fig.
At CK pulses other that pulse 8 of course, different sequences will occur, therefore there will be periods, as a change of value ripples through the chain of flip-flops, when unexpected values appear at the Q outputs for a very short time.
However this can cause problems when a particular binary 5 bit ripple counter with d is to be selected, as in the case of a decade counter, which must count from 2 to 2 9 10 and then reset to 2 on a 5 bit ripple counter with d of 2 10 These short-lived logic values will also cause a series of very short spikes on the Q outputs, as the propagation delay of a single flip-flop is only about to ns.
Although this problem prevents the circuit being used as a reliable counter, it is still valuable as a simple and effective frequency divider, where a high frequency oscillator provides the input and each flip-flop in the chain divides the frequency by two. The synchronous counter provides a more reliable circuit for counting purposes, and for high-speed operation, as the clock pulses in this circuit are fed to every flip-flop in the chain at exactly the same time.
Synchronous counters use JK flip-flops, as the programmable J and K inputs allow the toggling of individual flip-flops to be 5 bit ripple counter with d or disabled at various stages of the count. Synchronous counters therefore eliminate the clock ripple problem, as the operation of the circuit is synchronised 5 bit ripple counter with d the CK pulses, rather than flip-flop outputs. Notice that the CK input is applied to all the flip-flops in parallel. Therefore, as all the flip-flops receive a clock pulse at the same instant, some method must be used to prevent all the flip-flops changing state at the same time.
This of course would result in the counter outputs simply toggling from all ones to all zeros, and back again with each clock pulse.
However, with JK flip-flops, when both J and K inputs are logic 1 the output toggles on each CK pulse, but when J and K are 5 bit ripple counter with d at logic 0 no change takes place. The binary output is taken from the Q outputs of the flip-flops. Note that on FF0 the J and K inputs are permanently wired to logic 1, so Q 0 will change state toggle on each clock pulse.
In adding a third flip flop to the counter however, direct connection from J and K to the previous Q 1 output would not give 5 bit ripple counter with d correct count. Because Q 1 is high at a count of 2 10 this would mean that FF2 would toggle on clock pulse three, as J2 and K2 would be high. Therefore clock pulse 3 would give a binary count of 2 or 7 10 instead of 4 To prevent this problem an AND gate is used, as shown in Fig.
Only when the outputs are in this state will the next clock pulse toggle Q 2 to logic 1. The outputs Q 0 and Q 1 will of course return to logic 0 on this pulse, so giving a count of 2 or 4 10 with Q 0 being the least significant bit. Q 3 therefore will not toggle to its high state until the eighth clock pulse, and will remain high until the sixteenth clock pulse. After this pulse, all the Q outputs will return to zero.
Note that for this basic form of the synchronous counter to work, the PR and CLR inputs must also be all at logic 1, their inactive state as shown in Fig. Converting the synchronous up counter to count down is simply a matter of reversing the count. If all of the ones and zeros in the 0 to 15 10 sequence shown in Table 5. As every Q output on the JK flip-flops has its complement on Qall that is needed to convert the up counter in Fig.
Each group of 5 bit ripple counter with d between successive flip-flops is in fact a modified data select circuit described in Combinational Logic Module 4. This is necessary to provide the correct logic state for the next data selector. If the control input is at logic 1 then the CK pulse to the next flip-flop is fed from the Q output, making the counter an UP counter, but if the control input is 0 then CK pulses are fed from Q and the counter is a DOWN counter.
When Q 1 and Q 3 are both at logic 1, the output terminal of the limit detection NAND gate LD1 will become logic 0 and reset all the flip-flop outputs to logic 0. Because the first time Q 1 and Q 3 are both at logic 1 during a 0 to 15 10 count is at a count of ten 2this will cause the counter to count from 0 to 9 10 and then reset to 0, omitting 10 10 to 15 The circuit is therefore a BCD counter, an extremely useful device for driving numeric displays via a BCD to 7-segment decoder etc.
However by re-designing the gating system to produce logic 0 at the CLR inputs for a different maximum value, any count other than 0 to 15 can 5 bit ripple counter with d achieved. If you already have a simulator such as Logisim installed on your computer, why not try designing an Octal up counter for example. Although synchronous counters can be, and are built from individual JK flip-flops, in many circuits they will be ether built into dedicated counter ICs, or into other large scale integrated circuits LSICs.
For many applications the counters contained within ICs have extra inputs and outputs added to increase the counters versatility. The differences between many commercial counter ICs are basically the different input and output facilities offered.
Some of which are described below. Notice that many of these inputs are active low; this derives from the fact that in earlier TTL devices any unconnected input would float up to logic 1 and hence become inactive.
However leaving inputs un-connected is not good practice, especially CMOS inputs, which float between logic states, and could easily be activated to either valid logic state by random noise in the circuit, therefore ANY unused input should be permanently connected to its inactive logic state. Count Enable CTEN for example, is a feature on counter integrated circuits, and in the synchronous counter illustrated in Fig 5. When it is set to logic 1, it will prevent the count from progressing, even in the presence of clock pulses, but the count will continue normally when CTEN is at logic 0.
A common way of disabling the counter, whilst retaining any current data on the Q outputs, is to inhibit the toggle action of the JK flip-flops whilst CTEN is inactive logic 1by making the JK 5 bit ripple counter with d of all the flip-flops logic 0. When the count is disabled, CTEN and therefore one of the inputs on each ofE1, E2 and E3 will be at logic 0, which will cause these enable gate outputs, and the flip-flop JK inputs to also be at logic 0, whatever logic states are present on the Q outputs, and also at the other enable gate inputs.
Therefore whenever CTEN is 5 bit ripple counter with d logic 1 the count is disabled. In this condition, when the next clock pulse is received 5 bit ripple counter with d the CK input the flip-flops will toggle, following their normal sequence. Using a separate DATA input for each flip-flop, and a small amount of extra logic, a logic 0 on the PL will load the counter with any pre-determined binary value before the start of, or during the count.
A method of achieving asynchronous parallel loading on a synchronous counter is shown in Fig. The binary value to be loaded into the counter is applied to inputs D 0 to D 3 and a logic 0 pulse is applied to the PL input.
This logic 0 is inverted and applied to one input of each of the eight NAND gates to enable them. If the value to be loaded into a particular flip-flop is logic 1, this makes the inputs of the right hand NAND gate 1,1 and due to the 5 bit ripple counter with d between the pair of NAND gates for that particular input, the left hand NAND gate inputs will be 1,0. The result of this is that logic 0 is applied to the flip-flop PR input and logic 1 is applied to the CLR input.
This combination sets the Q output to logic 1, the same value that was applied to the D input. Similarly if a D input is at logic 0 the output of the left hand NAND gate of the pair will be Logic 0 and the right hand gate output will be logic 1, which will clear the Q output of the flip-flop. Because the PL input is common to each pair of load NAND gates, all four flip-flops are loaded simultaneously with the value, either 1 or 0 present at its particular D input. Modifications such as those described in this module make the basic synchronous counter much more versatile.
Both TTL and CMOS synchronous counters are available in the 74 series of ICs containing usually 4-bit counters with these and other modifications 5 bit ripple counter with d a wide variety of applications. Stops count without resetting when at logic 1. TC can be used to detect the end of an up or down count, and as well as being available as an output, TC is used internally to generate the Ripple Carry output.
Connecting Synchronous counters in cascade, to obtain greater count ranges, is made simple in ICs such as the 74HC by using the ripple carry RC output of the IC counting the least significant 4 bits, to drive the clock input of the next most significant IC, as show in red in Fig. Although it may appear that either the TC or the RC outputs could drive the next clock input, the TC output is not intended for this purpose, as timing issues can occur.
Although synchronous counters have a great advantage over asynchronous or ripple counters in regard to reducing timing problems, there are situations where ripple counters have an advantage over synchronous counters. When used at high speeds, only the first flip-flop in the ripple counter chain runs at the clock frequency. Each subsequent flip-flop runs at half the frequency of the previous one.
In synchronous counters, with every stage operating at very high clock frequencies, stray capacitive coupling between the counter and other components and within the counter itself is more likely occur, so that in synchronous counters interference can be transferred between different stages of the counter, upsetting the count if adequate decoupling is not provided.
This problem is reduced in ripple counters due to the lower frequencies in most of the stages. Also, because the clock pulses applied to synchronous 5 bit ripple counter with d must charge, and discharge the input capacitance of every flip-flop simultaneously; synchronous counters having many flip-flops will cause large pulses 5 bit ripple counter with d charge and discharge current in the clock driver circuits every time the clock changes logic state.
This can also cause unwelcome spikes on the supply lines that could cause problems elsewhere in the digital circuitry. This is less of a problem with asynchronous counters, as the clock is only driving the first flip-flop in the counter chain. Asynchronous counters are mostly used for frequency division applications and for generating time delays. In either of these applications the timing of individual outputs is not likely to cause a problem to external circuitry, and the fact that most of the stages in the counter run at much lower frequencies than the input clock, greatly reduces any 5 bit ripple counter with d of high frequency noise interference to surrounding components.
Hons All rights reserved. Learn about electronics Digital Electronics. After studying this section, you should be able to: Understand the operation of digital counter circuits and can: Describe the action of asynchronous ripple counters using D Type flip flops.
Understand the operation of synchronous counters. Describe common control features used in synchronous counters.
Use software to simulate counter operation.

Although it may be possible to mine for bitcoins using GPUs or ASIC hardware, these require significant investment which will put most people off. Op Ed: The 5 bit ripple counter with d of Trading Bots in the Cryptocurrency MarketFor example Haasbot will do most of the work for its users.
No different peek at cloth I used in conjunction with the Dumps.